Random Forest

Bagging is an ensemble algorithm that fits multiple models on different subsets of a training dataset, then combines the predictions from all models. Random forest is an extension of bagging that also randomly selects subsets of features used in each data sample. Both bagging and random forests have proven effective on a wide range of different predictive modeling problems.

Although effective, they are not suited to classification problems with a skewed class distribution. Nevertheless, many modifications to the algorithms have been proposed that adapt their behavior and make them better suited to a severe class imbalance.

Random Forest is a model made up of many decision trees. Rather than just simply averaging the prediction of trees (which we could call a “forest”), this model uses two key concepts that gives it the name random:

• Random sampling of training data points when building trees
• Random subsets of features considered when splitting nodes

Random Sampling

When training, each tree in a random forest learns from a random sample of the data points. The samples are drawn with replacement, known as bootstrapping, which means that some samples will be used multiple times in a single tree. The idea is that by training each tree on different samples, although each tree might have high variance with respect to a particular set of the training data, overall, the entire forest will have lower variance but not at the cost of increasing the bias.

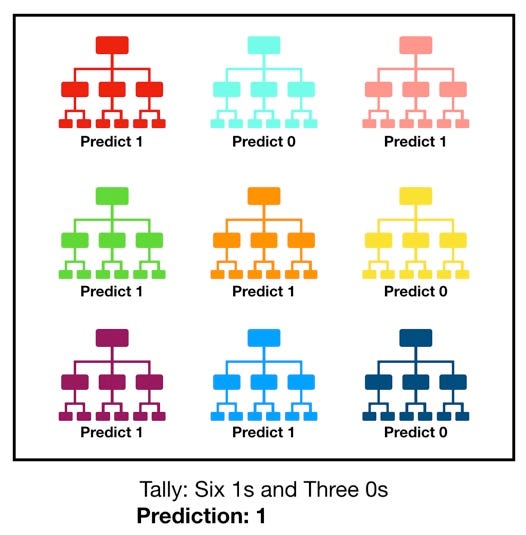
At test time, predictions are made by averaging the predictions of each decision tree. This procedure of training each individual learner on different bootstrapped subsets of the data and then averaging the predictions is known as bagging, short for bootstrap aggregating.

Random Subset

The other main concept in the random forest is that only a subset of all the features are considered for splitting each node in each decision tree. Generally this is set to $\sqrt{(n_features)}$ for classification meaning that if there are 16 features, at each node in each tree, only 4 random features will be considered for splitting the node. (The random forest can also be trained considering all the features at every node as is common in regression.

Conclusion

The random forest combines hundreds or thousands of decision trees, trains each one on a slightly different set of the observations, splitting nodes in each tree considering a limited number of the features. The final predictions of the random forest are made by averaging the predictions of each individual tree.

The reason for this wonderful effect is that the trees protect each other from their individual errors (as long as they don’t constantly all err in the same direction). While some trees may be wrong, many other trees will be right, so as a group the trees are able to move in the correct direction. So the prerequisites for random forest to perform well are:

1. There needs to be some actual signal in our features so that models built using those features do better than random guessing.
2. The predictions (and therefore the errors) made by the individual trees need to have low correlations with each other.